
Videoeinführung in dieses Kapitel
https://vimeo.com/482079741/3231748cac
4 Elementare Substitution
Im Übungsteil finden Sie folgende Aufgaben zum Training der in diesem Abschnitt behandelten Themen:
- Lineare Substitution (LSub): Aufgaben 5.5 (S.52) und 5.6 (S.54)
- Substitution zur Elimination der Ableitung (EdA): Aufgaben 5.7(S.55), 5.8 (S.57)
Fast unendlich viele weitere Trainingsmöglichkeiten bieten Ihnen die digitalen Aufgaben zu diesem Kapitel:
• zur Lineare Substitution (LSub)

Beliebig häufiges Üben mit digitalen Aufgaben!
1. Scannen Sie den QR-Code oder rufen Sie folgenden Link auf:
https://tinyurl.com/ycvwxtvh.
2. Klicken Sie dann auf: Kapitel 4.1 | Chapter 4.1
3. Klicken Sie anschließend auf ”Los geht’s!“.
• Substitution zur Elimination der Ableitung (EdA)

Beliebig häufiges Üben mit digitalen Aufgaben!
1. Scannen Sie den QR-Code oder rufen Sie folgenden Link auf:
https://tinyurl.com/ycvwxtvh.
2. Klicken Sie dann auf: Kapitel 4.2 | Chapter 4.2
3. Klicken Sie anschließend auf ”Los geht’s!“.
4.1 Lineare Substitution (LSub)
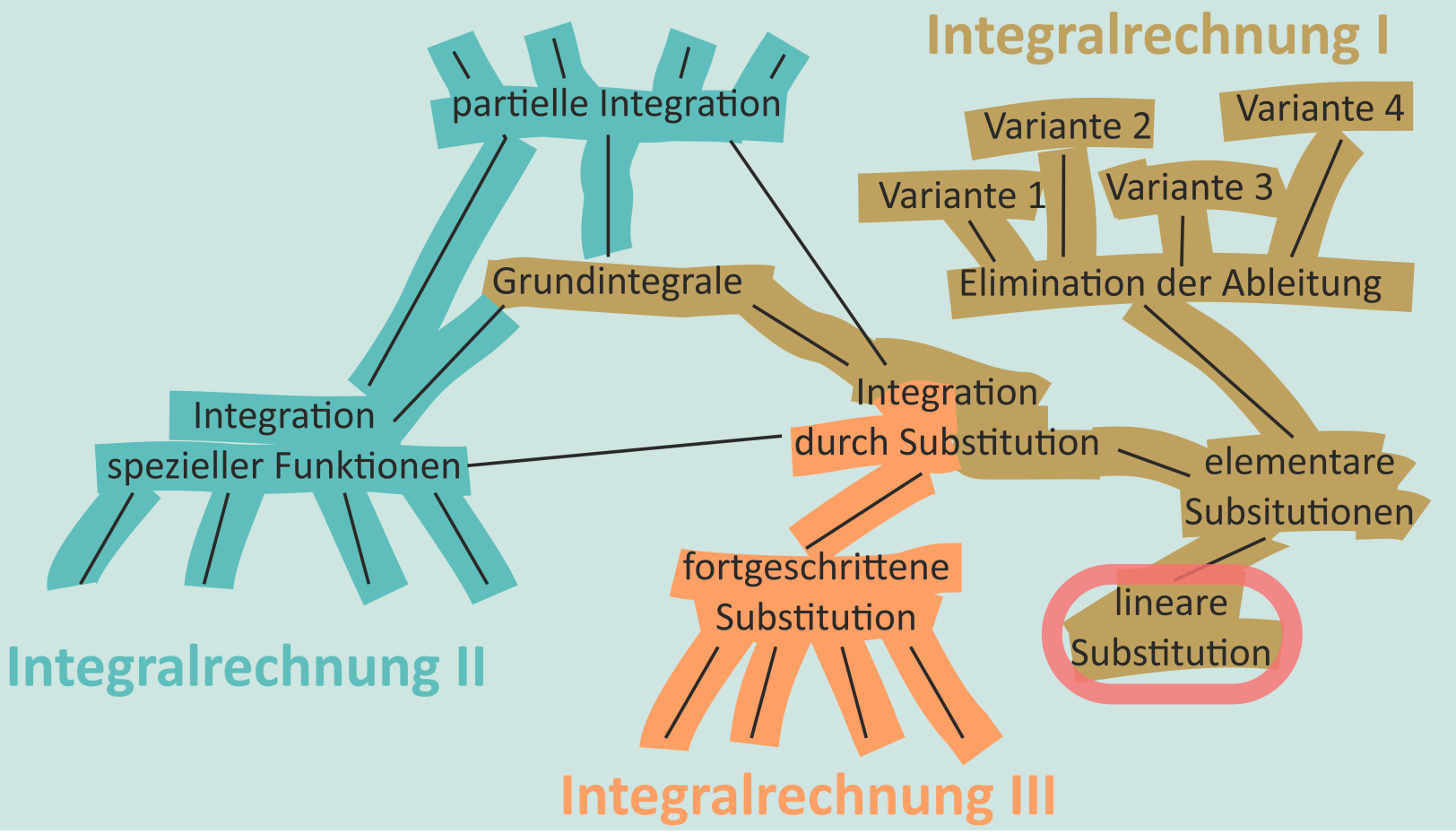
Abbildung 5: Methoden und Techniken der Integralrechnung
Beispiel 4.1
Berechnen Sie das Integral \(int cos (-3x+2), dx\).



Learning Nugget
https://vimeo.com/493746598/0c7d32ace9
Beispiel 4.2
Berechnen Sie das Integral \( int_{-1}^{-{2}{5}} e^{5x+2}, dx\)

Komponente Beispiel X.XX
Berechnen Sie das Integral \( int_{-1}^{-{2}{5}} e^{5x+2}, dx\)


Komponente Learning Nugget (100% Breite)
https://vimeo.com/493746598/0c7d32ace9

Komponente Learning Nugget (75% Breite)
https://vimeo.com/493746598/0c7d32ace9



